Our fluid dynamics professor, Lee, gave us the homework about how the viscosity is measured by conical viscometer. This is not that difficult problem if you know how to derive the surface area of rotating body and most importantly, the due date of this homework is right after tomorrow so let’s begin in a hurry.
The outline of Conical Viscometer is
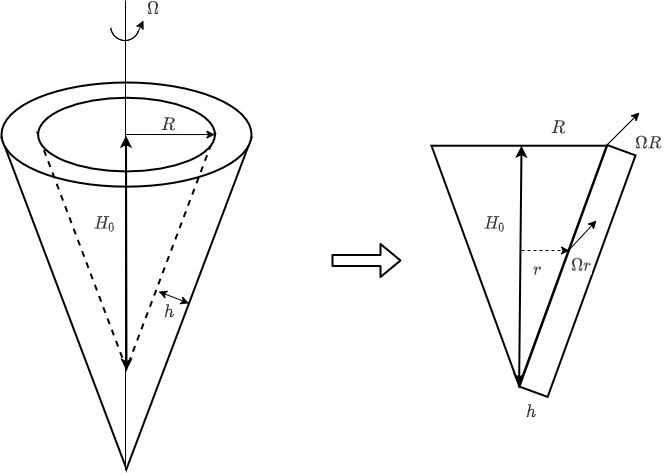
If we set shear stress as tau, tau is
\[\tau=\mu\frac{\Omega r}{h} \\ r\neq constant\]And the Force and Torque are
\[F=\int{\tau dA}\\dF=\tau dA\\ T=\int{rdF}\\dT=rdF\]On the other hand, the cone is rotating body.
To get the surface area of the cone, draw a graph.
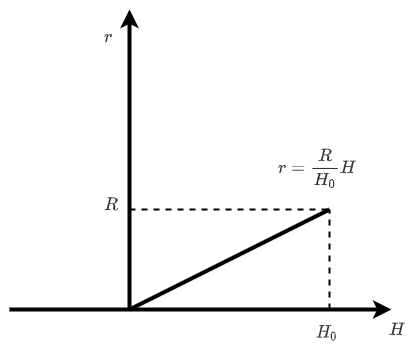
The micro unit of the surface area (dA) can be derived as
\[S=\int^{x}_0{2\pi f(x)\sqrt{1+\{f'(x)\}^2}dx}\\\therefore \ A=\int^{H'}_{0}{2\pi \frac{R}{H_0}H\sqrt{1+(\frac{R}{H_0})^2}dH} \\ dA=2\pi \frac{R}{H_0}H\sqrt{1+(\frac{R}{H_0})^2}dH\\dr = \frac{R}{H_0}dH\\\therefore dA=2\pi \frac{H_0}{R}r\sqrt{1+(\frac{R}{H_0})^2}dr\]Therefore, we can get Force and Torque.
\[F=\int{\tau dA}=\int^{R}_0{\frac{2\pi \mu \Omega H_0}{hR}r^2\sqrt{1+(\frac{R}{H_0})^2}dr} \\= \frac{2\pi \mu \Omega H_0R^2}{3h}\sqrt{1+(\frac{R}{H_0})^2} \\ dT=rdF=\frac{2\pi \mu \Omega H_0}{hR}r^3\sqrt{1+(\frac{R}{H_0})^2}dr \\ \therefore T=\int{rdF}=\int^{R}_0{\frac{2\pi \mu \Omega H_0}{hR}r^3\sqrt{1+(\frac{R}{H_0})^2}dr}\\=\frac{\pi \mu \Omega H_0R^3}{2h}\sqrt{1+(\frac{R}{H_0})^2}\\\frac{\pi \mu \Omega R^4}{2h}\sqrt{1+(\frac{H_0}{R})^2}\]