Let’s think about the river as this picture.
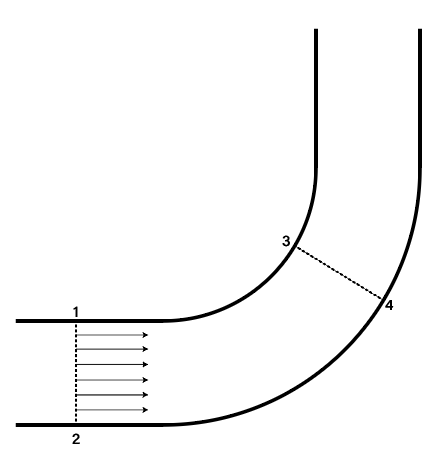
If we set the equation over 1 to 2 line,
\[\require{cancel} R \rightarrow \infty\\ \frac{P_1}{\rho}+\cancelto{0}{\int{\frac{V^2}{R}}dn}+\cancelto 0 {gz}=\frac{P_2}{\rho}+\cancelto{0}{\int{\frac{V^2}{R}}dn}+\cancelto 0 {gz}\\ \therefore P_1=P_2\]and consider the streamline 1 to 3 and 2 to 4,
\[\require{cancel} \frac{P_1}{\rho}+\frac12V_1^2+\cancelto0{gz}=C_{13}\\ \frac{P_2}{\rho}+\frac12V_2^2+\cancelto0{gz}=C_{24}\\ P_1=P_2,\ V_1=V_2\\ \therefore C_{13}=C_{24}\]All we know that
\[\frac{dP}{dR}=\frac{\rho V^2}{R}\\\]The relation of the $V_3$, $V_4$ and $P_3$, $P_4$ is
\[\frac{P_3}{\rho}+\frac12V_3^2=\frac{P_4}{\rho}+\frac12V_4^2\\ \because C_{13}=C_{24}\\\]Therefore,
\[\frac{dP}{dR}=\frac{\rho V^2}{R}\\ \therefore P_3 <P_4\\ if \ P_3<P_4, V_4<V_3\\ \therefore V_4<V_3 \dots Ans\]